

На первый взгляд, геометрия Лобачевского не согласуется с нашими привычными представлениями о геометрии пространства. Согласитесь, ведь непросто вообразить в уме несколько непересекающихся прямых на одной плоскости? А как насчет «треугольника», сумма углов которого менее 180°? Надо признать, что привычные геометрические представления здесь не работают. Дело в том, что геометрия Лобачевского описывает не плоское пространство, а пространство, имеющее некоторую отрицательную кривизну (т.е. имеется некоторое отрицательное значение, являющееся мерой кривизны в любой точке плоскости пространства). Не случайно сам ученый назвал свою теорию «воображаемой», ведь нужно обладать фантазией и пространственным воображением, чтобы представить такое гиперболическое пространство.
В XIX и начале XX века студенты, изучающие технические дисциплины, узнавали о представлении поверхностей при помощи решения уравнений на курсах аналитической геометрии твердого тела. Для иллюстрации таких поверхностей, учебные заведения зачастую приобретали модели в виде тех или иных геометрических тел. В Казанском университете сформировалась целая коллекция гипсовых моделей того времени. Сейчас её можно увидеть в экспозиции музея Н.И. Лобачевского.


Все фигуры изображают фрагменты плоскостей и имеют сложную форму. Среди них: псевдосфера, гиперболическсий параболоид, эллиптический конус, геликоид и др. Эти удобные модели помогают интуитивно понять геометрическую структуру плоскости. Если вы исследуете такую модель, то обнаружите, например, что треугольники на его поверхности имеют сумму углов, меньшую 180°.

Гипсовые фигуры могут выступать перед нами не только как музейные экспонаты, но и как средство практического освоения основных понятий неевклидовой геометрии. В этой связи, особое значение приобретает ограниченность восприятия посетителями предметов, невозможность взять в руки и рассмотреть их с разных сторон. Нередко у посетителей младшего и среднего возраста возникает желание «потрогать», «покрутить» фигуры. Чтобы упростить понимание замысловатой геометрической системы, было предложено визуализировать её трехмерными моделями. В этом случае исключается контакт с поверхностью объектов и никаким образом не отражается на сохранности.
В ближайшем времени уникальные экспонаты можно будет наблюдать не только «под стеклом» в статичном виде, но и просматривать их виртуальную версию, управлять видимостью, детально разглядеть и ознакомиться с дополнительной информацией о каждом объекте (размерах, названии, уравнении).
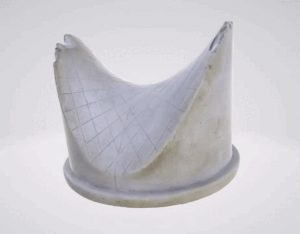
3D модель гипсовой фигуры гиперболического параболоида
Мы надеемся, что технологии трехмерного моделирования вызовут исследовательский интерес среди гостей нашего музея и напомнят о научных открытиях выдающихся математиков геометров. Ведь без геометрии невозможно задать поверхность в пространстве, без описания поверхности невозможно создать её представление в компьютерной графике с помощью полигонов и кривых. Все открытия, которые были сделаны математиками того времени, так или иначе, являются базисом современной трехмерной графики.
А как вы относитесь к идее создания реалистичных цифровых копий экспонатов музея?
В следующий раз мы подробнее остановимся на особенностях и перспективах внедрения 3D-технологий в современное пространство музеев Казанского университета.
Автор публикации: Юлия Солод